雅科夫•伊西达洛维奇•别莱利曼（1882—1942）

出生于俄国格罗德省别洛斯托克市，是享誉世界的科普作家、趣味科学的奠基人。17岁时，别莱利曼就开始在报刊上发表文章。1909年大学毕业后，开始全力从事科普写作和教育工作。

在别莱利曼的笔下，原本枯燥难懂的科学问题，变得妙趣横生、趣味十足，很容易引发青少年对科学的兴趣。他的许多作品被翻译成数十种语言，重印几十个版本，畅销不衰，对世界科普事业作出了非凡贡献。

说到数学谜题，你能想到多少个种类？你能想到的肯定没有作者多，在《趣味数学谜题》一书，作者用20章分门别类的介绍了排列与布局的谜题、拼剪谜题、交通谜题、数字谜题、魔方谜题、笔画谜题等20种类别、近230种不同的数学谜题，让我们一起去发现这个神奇的数学世界，去探索数学的魔力、发现数学的乐趣吧！s

书中既有实用的数学方法、解题方法，也有许多经典的数学问题和谜题。我们今天常见的很多数学难题，甚至“奥数”题，有少都来自于本书。

看过本书，你会发现，原来数学真的并不难，并且还会这么的有趣！

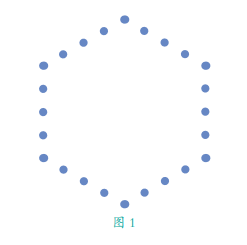
【题】不知道你们是否玩过这样一个小游戏，将 9 匹马安置在 10 个围栏中，而且保证每个围栏中都有一匹马。下面将要提到的这个问题与这个小游戏很像，这个问题就是：如何将 24 个人排成 6 排，并且保证每一排都有 5个人。

【解】这 24 个人按照图 1 的六边形排队，就能满足所有要求。

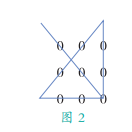
【题】如下排列的 9 个 0：

只用 4 条直线如何将这 9 个 0 全部勾掉，在勾掉 9 个 0 的时候笔尖不能

离开纸。

【解】答案如图 2 所示。

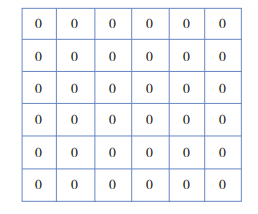
【题】请看下面方格中的 36 个 0，划掉 12 个 0，划掉后要保证横竖各行没有被划掉的 0 的数目相同。

应该划掉哪些 0 呢？

【解】36 个 0 划掉 12 个，会留下 24 个，也就是每一排留下 4 个。没有被划掉的 0 应该如下排列：

【题】将两个不同的棋子放在空的棋盘上，它们在棋盘上能摆出多少种不同的位置？

【解】第一枚棋子可以放在棋盘上的任何一个空白位置，即有 64 种方法。第一枚棋子放好后，第二枚棋子就剩下 63 个可以任意放的空白位置。也就是说，第一枚棋子的任意 64 种放法中的每一种都可以通过第二枚棋子变换出 63 种放法，由此可以得出摆放两枚棋子的方法总数：64×63=4 032。

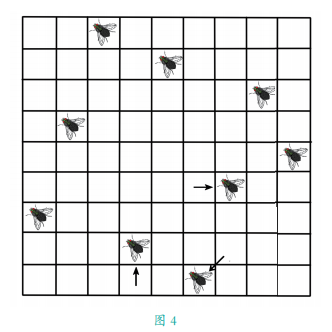
【题】有 9 只苍蝇停留在窗帘的正方形格子图案上，此刻它们所在的位置如图 3 所示，任意两只苍蝇都不在同一直线或者斜线上。

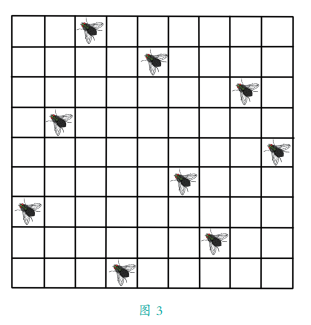
过了几分钟，有 3 只苍蝇爬到了中间空着的方格中，剩下的 6 只没有动，还保持在原来的位置。巧妙的是，尽管有 3 只苍蝇移动了位置，但是最后 9只苍蝇所处的位置，仍然是任意两只苍蝇都不在同一直线或者斜线上。

你知道那 3 只苍蝇是怎么移动的吗？

【解】找到图 4 中的箭头，箭头所在的方格是原来苍蝇所在的位置，箭头指示的方格就是苍蝇移动后所在的位置。

小贴士

科学家通过研究苍蝇的眼睛发明了很多利于人们生活的仿生仪器，比如：发明制造出“蝇眼”照相机，被用来复制计算机的显微电路；测量物体运动速度的光学测速仪；国防上用的“紫外眼”；等。